今回は、2025年度 千葉工業大学（A日程）数学
の入試問題を分析してみました。

千葉工大は、千葉県内の理系志望の生徒さんにとって、とても人気の高い大学です。

だからこそ保護者の方からは、

• 「どのくらいのレベルの数学力があれば、千葉工大に届くのか」

• 「学校のテストで“そこそこ”取れていれば大丈夫なのか」

といったご相談をよくいただきます。

今年の本試験を見た結論を先に言うと――

難問奇問は少なく、教科書〜標準問題の完成度で差がつく入試
ただし、分野が広く、計算を正確かつ素早くこなせるかが勝負

という印象がとても強い問題でした。

この記事では、

• どんな内容が出題されたのか

• そこから見える「千葉工大が求める数学力」

• いつ頃までに、どんな準備をしておきたいか

を、保護者の方にも分かりやすい形でまとめていきます。

1．千葉工大・数学入試のざっくり構成

■ 試験の基本情報

• 対象学部：工・創造工・先進工・情報変革科・未来変革科（A日程）

• 試験時間：80分

• 形式：全問マークシート

• 出題範囲：

  • 数学Ⅰ・Ⅱ

  • 数学A … 場合の数と確率 ＋ 図形の性質（角の二等分線）

  • 数学B … 数列

  • 数学C … ベクトル

  • ※数学Ⅲは出題されません。その分、数IA・IIBの完成度が純粋に問われます。

■ 問題構成（全4題）

1. 小問集合（計算・図形・ベクトル・積分）

2. 確率 ＋ 対数関数とグラフ

3. 数列（部分分数分解）＋ 三角関数（2次不等式への帰着）

4. 微分積分（3次関数と放物線の接線・面積）

解答解説には「基礎」「標準」といったラベルが付いており、
実際に見ても教科書〜標準問題集レベルが中心です。

一方で、

• 出題分野がかなり幅広い

• 80分で4題すべてマークする必要がある

という点から、
“少し難しい問題を解き切る力”よりも、“標準問題を落とさない力” が強く求められていることが分かります。

2．大問ごとの特徴と「差がつくポイント」

(1) 問1：小問集合 ― 「広く・浅く」ではなく「広く・正確に」

8問の小問で、

• 複素数の計算（分母の有理化）

• 二項定理の定数項

• 放物線の平行移動

• 円と三角形の性質（正弦定理・余弦定理を使う場面あり）

• 直線と円の接する条件（点と直線の距離）

• 角の二等分線・内心の性質（数A 図形の性質）

• ベクトルの内積

• 定積分∫-1^2 (x^3 + 3x^2 – 5) dx

などが、まんべんなく出題されています。

いずれも教科書の章末問題や標準問題集の例題レベルですが、

「どれか一つでも捨て単元がある」
＝ ここだけで大きく失点

という構成になっています。

特に、

• 数A「図形の性質」（内心・角の二等分線）

• 数C「ベクトル」

は、学校によって扱いの差が大きく、
「授業でサラッと流して終わり」になっていると危険な単元です。

(2) 問2：確率 ＋ 対数グラフ ― 「読み違え」と「変数変換」

■ 確率（反復試行と条件付き確率）

7枚のカードを2回引く問題で、

• 事象A … 2回とも奇数

• 事象B … 3の倍数のカードがちょうど1回

このとき

「A ∪ B が起こったとき、A ∩ B が起こっていない条件付き確率」

を求める問題でした。

ここで怖いのは、

• 「A ∩ B が起こる確率」

• 「A ∩ B が起こったときの条件付き確率」

と読み違えてしまうことです。

今年の問題は計算自体は難しくありませんが、

文末まで丁寧に読み、「何を聞かれているのか」を正確に捉える力

が試されています。

■ 対数とグラフ

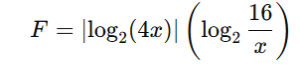
という式を、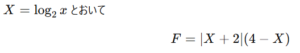

という絶対値付き2次関数にしてから、

• F の最大値

• 方程式 $F=k$ が3個の解をもつ k の範囲

を調べる問題でした。

ここで問われているのは、

• 「対数 → 変数変換 → グラフ」という典型パターンへの慣れ

• 絶対値付きの2次関数のグラフをイメージして、
  必要な情報を読み取る力

です。

(3) 問3：数列の和 と 三角関数

■ 分数式の恒等式と部分分数分解

​

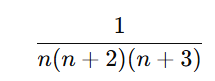
を「差の形」に分解して、
和をとると中間項が次々と消えていく、いわゆる望遠鏡型の和。

教科書でも扱う典型的なパターンですが、

• インデックスのずれ

• 分母の形の違い

を整理しながら計算する必要があります。

■ 三角関数（変数変換と2次不等式）

​

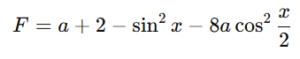
を変形し、

• 半角の公式で cosx に統一

• $t=\cos x(-1\le t\le 1)$ とおいて t の2次式に

最後は、

「−1≤t≤1のすべての t に対して2次式が正になるような a の範囲」

を求める、という数Ⅰの2次関数の応用問題に帰着します。

ここは今年のセットの中ではやや難しめで、

• 三角関数を代数の問題に“落とし込む”発想

• 2次関数の最大・最小や解の配置の知識

までしっかり身についているかどうかで、差がつく1問でした。

(4) 問4：3次関数と放物線の接線・面積

• 接線の方程式

• 共通接線の条件から k の最小値

• 囲まれた部分の面積

を求める構成です。

数Ⅲではなく数Ⅱ範囲の微分積分ですが、

• 接線の公式

• 接線が別の曲線にも接する条件（判別式の利用）

• グラフの交点から面積を定積分で求める

といった「教科書に載っている流れ」を、
時間内にきちんと書き切れるかがポイントです。

3．千葉工大が数学で見ている力

今年の出題から分かる、千葉工業大学の数学で重視されているポイントを整理すると、次の3つにまとまります。

①「基礎〜標準問題」を広い範囲で落とさないこと

• 単元は、数ⅠA・ⅡB・C のほぼフルセット

• 小問集合＋確率＋対数＋数列＋三角関数＋微積…と、苦手があるとすぐに点を落としてしまう構成です。

「この単元はやってない」「ここは苦手なのでスルー」という状態だと、
合格点を取りに行くのはかなり厳しいと言えます。

② 計算を正確に、スピーディーに

• 80分で4題・マーク式

• 整式の展開、分数計算、定積分など、途中計算はそれなりの量があります。

「考え方は合っているのに、計算ミスでマークを落とす」ことが続くと、
実力よりだいぶ低い点になってしまうタイプの試験です。

③ 問題文を“そのまま”読めるか

• 条件付き確率で「起こっていない」場合を聞いてくる

• 対数の係数や、変数の範囲が細かく指定されている

など、「ちゃんと読んでいれば解けるけれど、流し読みすると落とす」ポイントがいくつもありました。

数学＝計算力だけでなく、
国語力（読解力）も同時に試されていると感じます。

4．いつから、どんな準備をしておくと安心か

学年別に、ざっくりとした目安を書いてみます。

高1・高2のうちにしておきたいこと

• 数ⅠA・ⅡB の基本問題はほぼノーミスで解けるレベルまで仕上げる

• 「図形の性質」「ベクトル」「確率」「数列」などを、
  どれか一つでも「完全な苦手」にしない

• 計算の途中式を丁寧に書く習慣をつける
  → マーク式とはいえ、頭の中だけで処理しようとするとミスの元になります

高3で意識したいこと

• 千葉工大レベルの私大入試問題（標準〜やや難）を時間を測って解く

• 典型パターンを“自動化”しておく

  • 対数の変数変換

  • 部分分数分解と望遠鏡型の和

  • 三角関数から2次不等式への帰着

  • 微分→接線→共通接線

• 過去問や模試で、「読み違えミス」「計算ミス」をチェックし、
  なぜ間違えたかを具体的に振り返ること

5．「うちの子は千葉工大を目指せる？」と感じたら

今年の千葉工大数学は、

「難しさ」よりも「抜けのなさ」と「丁寧さ・速さ」が問われる入試

でした。

逆に言えば、

• 今は定期テストで“平均前後”でも、

• 基礎をコツコツ積み上げて、

• 典型問題をしっかり身につけていけば、

千葉工大レベルの数学には十分届く可能性があるということでもあります。

• 「うちの子の今の力で、千葉工大を目指せるのか知りたい」

• 「数ⅠA・ⅡBまではなんとなく出来るけれど、数列や確率が不安」

• 「計算ミスが多くて、模試で点数が安定しない」

といったお悩みがありましたら、
一度、学習状況のチェックと学習相談にお越しください。

• 現在の成績・苦手単元

• 志望学部・将来の進路

• 共通テスト・一般入試までのスケジュール

などを伺いながら、

「今年から何を・どの順番でやっていけば千葉工大レベルに届くのか」

を、お子さんと一緒に具体的に整理していきます。

千葉工業大学を一つの目標にしつつ、
その先の進路の選択肢も広がるような数学力を、一歩ずつ育てていきましょう。